
Game objects are the foundational components of a Unity game project. Every item that exists in a scene is, or is based on, a game object. In this hour, you learn about game objects within Unity. Before you can start working with objects in Unity, however, you must first learn about the 2D and 3D coordinate systems. Then you will begin working with the built-in Unity game objects, and you will wrap up the hour by learning about the various game object transformations. Information gained in this hour is foundational to everything else in this book. Be sure to take your time and learn it well.
Note: Learning About 2D and 3D
Unity is a 3D engine. Therefore, all the projects made with it will inherently use all three dimensions. You might be wondering why we bother to cover 2D systems at all. The truth is that even in 3D projects, there are still a lot of 2D elements. Textures, screen elements, and mapping techniques all use a 2D system. Unity has a powerful set of tools to work with 2D games, and 2D systems aren’t going away any time soon.
For all of their glitz and glamour, video games are mathematical constructs. All the properties, movements, and interactions can be boiled down to numbers. Luckily for you, a lot of the groundwork has already been laid. Mathematicians have been toiling away for centuries to discover, invent, and simplify different processes so that you can more easily build your games with modern software. You may think the objects in a game just exist in space randomly, but really every game space has dimensions, and every object is placed in a coordinate system (or grid).
As mentioned previously, every game uses some level of dimensions. The most common dimension systems, the ones you are most likely familiar with, are 2D and 3D (short for two-dimensional and three-dimensional). A 2D system is a flat system. In a 2D system, you deal only with vertical and horizontal elements (or to put it another way: up, down, left, and right). Games like Tetris, Pong, and Pac Man are good examples of 2D games. A 3D system is like a 2D system, but it obviously has one more dimension. In a 3D system, you have not only horizontal and vertical (up, down, left, and right), but also depth (in and out). Figure 2.1 does a good job of illustrating the difference between a 2D square and a 3D square, otherwise known as a cube. Notice how the inclusion of the depth axis in the 3D cube makes it seem to “pop out.”
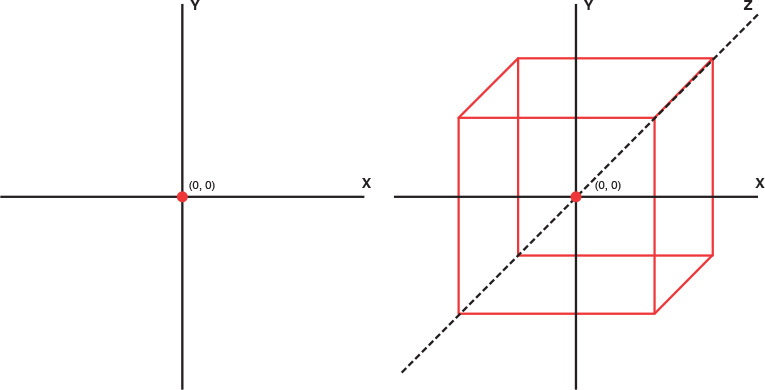
FIGURE 2.1 2D square versus 3D cube.
Note: Common Coordinate Syntax
When referring to an object’s position, you will generally list its coordinates. Saying that an object is 2 on the x axis and 4 on the y axis can be a little cumbersome. Luckily, a shorthand way of writing coordinates exists. In a 2D system, you write coordinates like (x, y), and in a 3D system, you write them like (x, y, z). Therefore, this example would instead be written as (2, 4). If that object were also 10 on the z axis, it would be written as (2, 4, 10).
The mathematical equivalent of a dimension system is a coordinate system. A coordinate system uses a series of lines, called axes (the plural of axis), and locations, called points. These axes correspond directly with the dimensions that they mimic. For instance, a 2D coordinate system has the x axis and y axis, which represent the horizontal and vertical directions, respectively. If an object is moving horizontally, we say it is moving “along the x axis.” Likewise, the 3D coordinate system uses the x axis, the y axis, and the z axis for horizontal, vertical, and depth, respectively.
Every coordinate system has a point where all the axes intersect. This point is called the origin, and the coordinates for the origin are always (0, 0) in a 2D system and (0, 0, 0) in a 3D system. This origin point is very important because it is the basis by which all other points are derived. The coordinates for any other point are simply the distance of that point from the origin along each axis. A point’s coordinates will get larger as it moves away from the origin. For example, as a point moves to the right, its x axis value gets larger. When it moves left, the x axis value gets smaller until it passes through the origin. At that time, the x value of the point begins getting larger again, but it also becomes negative. Consider Figure 2.2. This 2D coordinate system has three points defined. The point (2, 2) is 2 units away from the origin in both the x and y directions. The point (–3, 3) is 3 units to the left of the origin and 3 units above the origin. The point (2, –2) is 2 units to the right of the origin and 2 units below the origin.
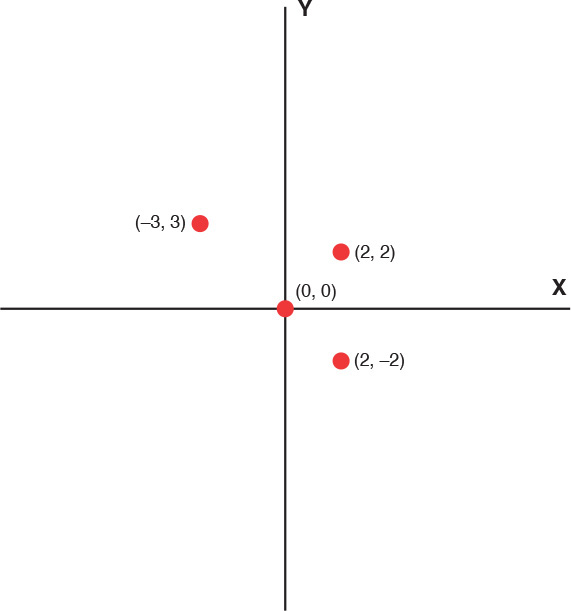
FIGURE 2.2 Points in relation to the origin.
You have now learned about the dimensions of a game world and about the coordinate systems that compose them. What you have been working with so far is considered the world coordinate system. At any given time, there is only a single x, y, and z axis in the world coordinate system. Likewise, there is only one origin that all objects share. What you might not know is that there is also something called the local coordinate system. This system is unique to each object, and it is completely separate from other objects. This local system has its own axes and origin that other objects don’t use. Figure 2.3 illustrates the world versus local coordinate systems by showing the four points that make of a square for each.
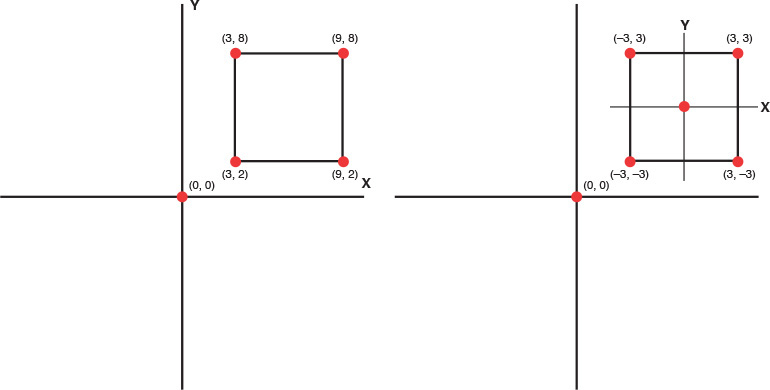
FIGURE 2.3 World coordinates versus local coordinates.
Note: Built-In Objects
Not every game object you use will start as an empty object. Unity has several built-in game objects available to use right out of the box. You can see the large amount of items available by clicking the GameObject menu item at the top of the Unity editor. A large portion of learning to use Unity is learning to work with built-in and custom game objects.
You might be wondering what the local coordinate system is for if the world coordinate system is used for the position of objects. Later in this hour, you will look at transforming game objects and at parenting game objects. Both of these require the local coordinate system.
Every shape, model, light, camera, particle system, and so on in a Unity game all have one thing in common: They are all game objects. The game object is the fundamental unit of any scene. Even though they are simple, they are very powerful. At their root, game objects are little more than a transform (as discussed in greater detail later in the hour) and a container. This container exists to hold the various components that make objects more dynamic and meaningful. What you add to your game objects is up to you. There are many components, and they add a huge amount of variety. Throughout the course of this book, you will be learning to use many of these components.
Tip: About Rect Transforms
2D objects in Unity have a different type of transform, called a rect transform. We cover this later in the book in more detail; for now, just understand that they are the 2D equivalent of the other three tools.
Tip: The Transform Component and Transform Tools
Unity provides two ways to manage the transform of your objects. Knowing when to use each is important. You will notice that when you change an object’s transform in the Scene view with a transform tool, the transform data also changes in the Inspector view. It is often easier to make large changes to an object’s transform using the Inspector view because you can just change the values to what they need to be. The transform tools, however, are more useful for quick, small changes. Learning to use both together will greatly improve your workflow.
At this point, you have learned and explored the different coordinate systems and experimented with some game objects. It is time to put the two together. When dealing with 3D objects, you will often hear the term transform. Depending on the context, transform is either a noun or a verb. All objects in 3D space have a position, a rotation, and a scale. If you combine them all together, you get an object’s transform (noun). Alternatively, transform can be a verb if it refers to changing an object’s position, rotation, or scale. Unity combines the two meanings of the word with the transform component.
You will recall that the transform component is the only component that every game object has to have. Even empty game objects have transforms. Using this component, you can both see the current transform of the object and change (or transform) the transform of the object. It might sound confusing now, but it is fairly simple. You will get the hang of it in no time. Because the transform is made up of the position, rotation, and scale, it stands to reason that there are three separate methods (called transformations) of changing the transform: translation, rotation, and scaling (respectively). These transformations can be achieved using either the Inspector or the transform tools. Figures 2.4 and 2.5 illustrate which Inspector components and tools correlate with which transforms.
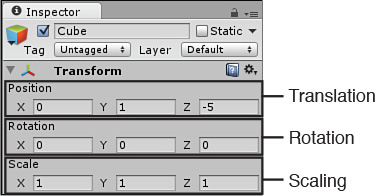
FIGURE 2.4 Transform options in the Inspector.
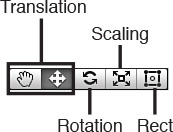
FIGURE 2.5 The transform tools.
Changing the coordinate position of an object in a 3D system is called translation, and it is the simplest transform that you can apply to an object. When you translate an object, it is shifted along an axis. Figure 2.6 demonstrates a square being translated along the x axis.
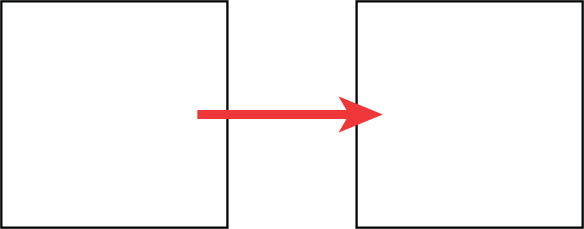
FIGURE 2.6 Sample translation.
When you select the Translate tool (hotkey: w), you will notice that whatever object you have selected will change slightly in the Scene view. More specifically, you will see three arrows appear pointing away from the center of the object along the three axes. These are translation gizmos, and they help you move your objects around in the scene. Clicking on and holding any of these axis arrows causes them to turn yellow. Then, if you move your mouse, the object will move along that axis. Figure 2.7 shows you what the translation gizmos look like. Note that the gizmos appear only in the Scene view; if you are in the Game view, you will not see them.
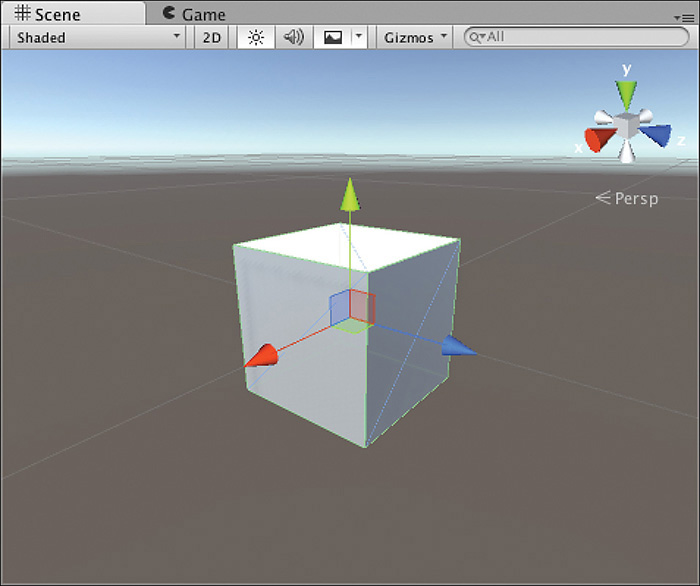
FIGURE 2.7 Translation gizmos.
Rotating an object does not move it in space. Instead, it changes the object’s relationship to that space. More simply stated, rotation enables you to redefine which direction the x, y, and z axes point for a particular object. When an object rotates around an axis, it is said to be rotating about that axis. Figure 2.8 shows a square being rotated about the z axis.
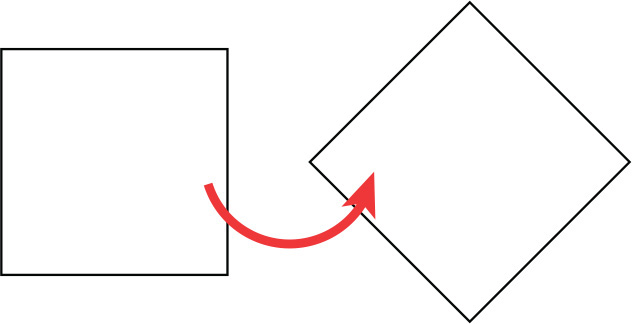
FIGURE 2.8 Rotation about the z axis.
Tip: Determining the Axis of Rotation
If you are unsure which axis you need to rotate an object about to get a desired effect, you can use a simple mental method. One axis at a time, pretend that the object is stuck in place by a pin that is parallel with that axis. The object can only spin around the pin stuck in it. Now, determine which pin allows the object to spin the way you want. That is the axis you need to rotate the object about.
Just as with the Translate tool, selecting the Rotate tool (hotkey: e) causes rotation gizmos to appear around your object. These gizmos are circles representing the object’s rotation path about the axes. Clicking and dragging on any of these circles turns them yellow and rotates the object about that axis. Figure 2.9 shows you what the rotation gizmos look like.
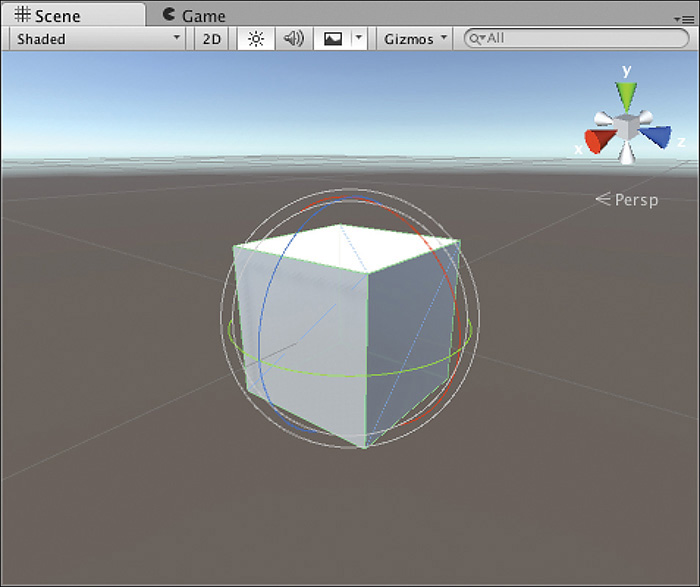
FIGURE 2.9 The Rotate tool gizmos.
Scaling causes an object to grow or shrink within a 3D space. This transform is really straightforward and simple in its use. Scaling an object on any axis causes its size to change on that axis. Figure 2.10 demonstrates a square being scaled down on the x and y axes. Figure 2.11 shows you what the scaling gizmos look like when you select the Scaling tool (hotkey: r).
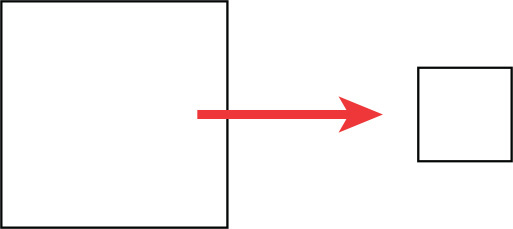
FIGURE 2.10 Scaling on the x and y axes.
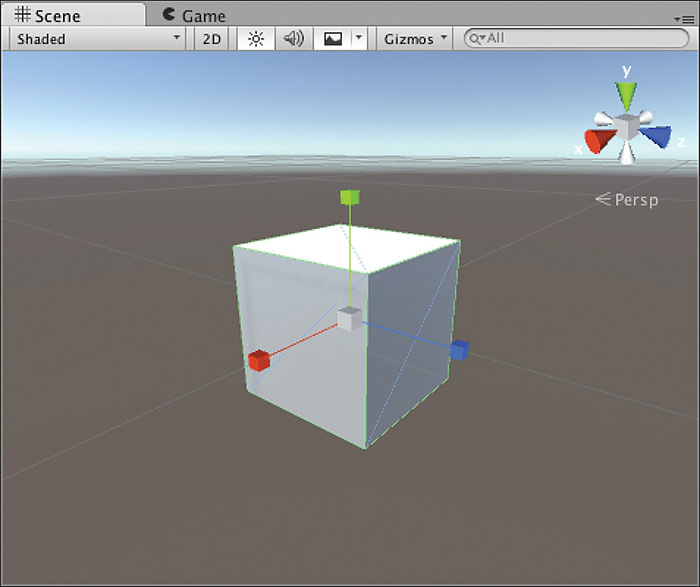
FIGURE 2.11 The scaling gizmos.
As mentioned before, transformations use the local coordinate system. Therefore, the changes that are made can potentially impact future transformations. Consider Figure 2.12. Notice how the same two transformations, when applied in reverse order, have very different effects.
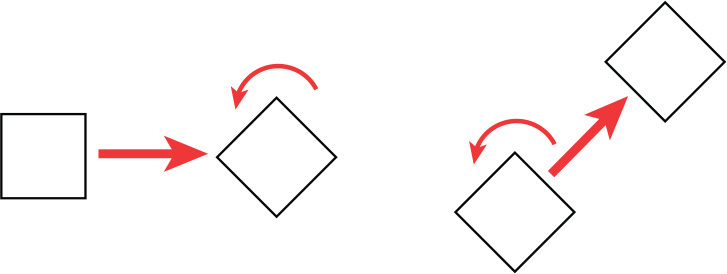
FIGURE 2.12 Effects of transformation order.
As you can see, not paying attention to transformation order can have unexpected consequences. Luckily, the transformations have consistent effects that can be planned on:
Once you understand these rules, determining how an object will change with a set of transformations becomes easy. These effects depend on whether we have Local or Global selected, and take some getting used to, so the best thing is to experiment.
In Hour 1, “Introduction to Unity,” you learned how to nest game objects in the Hierarchy view (drag one object onto another one). Recall that when you have an object nested inside another one, the top-level object is the parent, and the other object is the child. Transformations applied to the parent object work as normal. The object can be moved, scaled, and rotated. What’s special is how the child object behaves. Once nested, a child object’s transform is relative to that of the parent object, not the world. Therefore, a child object position is not based on its distance from the origin, but the distance from the parent object. If the parent object is rotated, the child object would move with it. If you looked at the child’s rotation, however, it would not register that it had rotated at all. The same goes for scaling. If you scale the parent object, the child also changes in size. The scale of the child object would remain unchanged. You might be confused by why this is. Remember, when a transformation is applied, it is not applied to the object, but to the object’s coordinate system. An object isn’t rotated, its coordinate system is. The effect is that the object turns. When a child object’s coordinate system is based on the local coordinate system of the parent, any changes to the parent system will directly change the child (without the child knowing about it).
In this hour, you learned all about game objects in Unity. You started off by learning all about the differences between 2D and 3D. From there, you looked at the coordinate system and how it breaks the “world” concepts down mathematically. You then began working with game objects, including some of the built-in ones. You ended by learning all about transforms and the three transformations. You got to try out the transforms, learn about some of the hazards, and how they affect nested objects.
Q. Is it important to learn both the 2D and 3D concepts?
A. Yes. Even games that are entirely 3D still utilize some of the 2D concepts on a technical level.
Q. Should I learn to use all the built-in game objects right away?
A. Not necessarily. There are many game objects, and it can be overwhelming to attempt to learn them all right away. Take your time and learn about the objects as they are covered here.
Q. What is the best way to get familiar with transforms?
A. Practice. Keep working with them; eventually, they will become quite natural.
Take a moment to experiment with the way transformations work in a parent/child object scenario. You will get a better feel for exactly how the coordinate systems change the way things are oriented.
1. Create a new scene or project.
2. Add a cube to the project and place it at (0, 2, –5). Remember the shorthand notation for coordinates. The cube should have an x value of 0, a y value of 2, and a z value of –5. You can set these values easily in the transform component in the Inspector view.
3. Add a sphere to your scene. Pay attention to the sphere’s x, y, and z values.
4. Nest the sphere under the cube by dragging the sphere in the Hierarchy view onto the cube. Notice how the position values changed. The sphere is now located relative to the cube.
5. Place the sphere at (0, 1, 0). Notice how it doesn’t go to right above the origin and instead sits right above the cube.
6. Now experiment with the various transformations. Be sure to try them on the cube as well as the sphere and see how differently they behave for a parent versus a child object.