
The true power of programs you create is their manipulation of data. In order to truly take advantage of this power, you need to better understand the different data types you can use, as well as how to create and name variables. C has a rich variety of math operators that you can use to manipulate your data. In this chapter you will cover:
int, float, double, char, and _Bool data typesshort, long, and long longYou have already been exposed to the C basic data type int. As you will recall, a variable declared to be of type int can be used to contain integral values only—that is, values that do not contain decimal places.
The C programming language provides four other basic data types: float, double, char, and _Bool. A variable declared to be of type float can be used for storing floating-point numbers (values containing decimal places). The double type is the same as type float, only with roughly twice the precision. The char data type can be used to store a single character, such as the letter ’a’, the digit character ’6’, or a semicolon (’;’) (more on this later). Finally, the _Bool data type can be used to store just the values 0 or 1. Variables of this type are used for indicating an on/off, yes/no, or true/false situation. These one-or-the-other choices are also known as binary choices.
In C, any number, single character, or character string is known as a constant. For example, the number 58 represents a constant integer value. The character string "Programming in C is fun.\n" is an example of a constant character string. Expressions consisting entirely of constant values are called constant expressions. So, the expression
128 + 7 - 17
is a constant expression because each of the terms of the expression is a constant value. But if i were declared to be an integer variable, the expression
128 + 7 – i
would not represent a constant expression because its value would change based on the value of i. If i is 10, the expression is equal to 125, but if i is 200, the expression is equal to −65.
In C, an integer constant consists of a sequence of one or more digits. A minus sign preceding the sequence indicates that the value is negative. The values 158, −10, and 0 are all valid examples of integer constants. No embedded spaces are permitted between the digits, and values larger than 999 cannot be expressed using commas. (So, the value 12,000 is not a valid integer constant and must be written as 12000.)
Two special formats in C enable integer constants to be expressed in a base other than decimal (base 10). If the first digit of the integer value is a 0, the integer is taken as expressed in octal notation—that is, in base 8. In that case, the remaining digits of the value must be valid base-8 digits and, therefore, must be 0–7. So, to express the value 50 in base 8 in C, which is equivalent to the value 40 in decimal, the notation 050 is used. Similarly, the octal constant 0177 represents the decimal value 127 (1 × 64 + 7 × 8 + 7). An integer value can be displayed at the terminal in octal notation by using the format characters %o in the format string of a printf() statement. In such a case, the value is displayed in octal without a leading zero. The format character %#o does cause a leading zero to be displayed before an octal value.
If an integer constant is preceded by a zero and the letter x (either lowercase or uppercase), the value is taken as being expressed in hexadecimal (base 16) notation. Immediately following the letter x are the digits of the hexadecimal value, which can be composed of the digits 0–9 and the letters a–f (or A–F). The letters represent the values 10–15, respectively. So, to assign the hexadecimal value FFEF0D to an integer variable called rgbColor, the statement
rgbColor = 0xFFEF0D;
can be used. The format characters %x display a value in hexadecimal format without the leading 0x, and using lowercase letters a–f for hexadecimal digits. To display the value with the leading 0x, you use the format characters %#x, as in the following:
printf ("Color is %#x\n", rgbColor);
An uppercase x, as in %X or %#X, can be used to display the leading x and the hexadecimal digits that follow using uppercase letters.
Every value, whether it’s a character, integer, or floating-point number, has a range of values associated with it. This range has to do with the amount of storage that is allocated to store a particular type of data. In general, that amount is not defined in the language. It typically depends on the computer you’re running, and is, therefore, called implementation- or machine-dependent. For example, an integer might take up 32 bits on your computer, or perhaps it might be stored in 64. You should never write programs that make any assumptions about the size of your data types. You are, however, guaranteed that a minimum amount of storage will be set aside for each basic data type. For example, it’s guaranteed that an integer value will be stored in a minimum of 32 bits of storage, which is the size of a “word” on many computers.
A variable declared to be of type float can be used for storing values containing decimal places. A floating-point constant is distinguished by the presence of a decimal point. You can omit digits before the decimal point or digits after the decimal point, but obviously you can’t omit both. The values 3., 125.8, and −.0001 are all valid examples of floating-point constants. To display a floating-point value at the terminal, the printf conversion characters %f are used.
Floating-point constants can also be expressed in scientific notation. The value 1.7e4 is a floating-point value expressed in this notation and represents the value 1.7 × 104. The value before the letter e is known as the mantissa, whereas the value that follows is called the exponent. This exponent, which can be preceded by an optional plus or minus sign, represents the power of 10 by which the mantissa is to be multiplied. So, in the constant 2.25e−3, the 2.25 is the value of the mantissa and −3 is the value of the exponent. This constant represents the value 2.25 × 10−3, or 0.00225. Incidentally, the letter e, which separates the mantissa from the exponent, can be written in either lowercase or uppercase.
To display a value in scientific notation, the format characters %e should be specified in the printf() format string. The printf() format characters %g can be used to let printf() decide whether to display the floating-point value in normal floating-point notation or in scientific notation. This decision is based on the value of the exponent: If it’s less than −4 or greater than 5, %e (scientific notation) format is used; otherwise, %f format is used.
Use the %g format characters for displaying floating-point numbers—it produces the most aesthetically pleasing output.
A hexadecimal floating constant consists of a leading 0x or 0X, followed by one or more decimal or hexadecimal digits, followed by a p or P, followed by an optionally signed binary exponent. For example, 0x0.3p10 represents the value 3/16 × 210 = 0.5.
The double type is very similar to the float type, but it is used whenever the range provided by a float variable is not sufficient. Variables declared to be of type double can store roughly twice as many significant digits as can a variable of type float. Most computers represent double values using 64 bits.
Unless told otherwise, all floating-point constants are taken as double values by the C compiler. To explicitly express a float constant, append either an f or F to the end of the number, as follows:
12.5f
To display a double value, the format characters %f, %e, or %g, which are the same format characters used to display a float value, can be used.
A char variable can be used to store a single character.1 A character constant is formed by enclosing the character within a pair of single quotation marks. So 'a', ';', and '0' are all valid examples of character constants. The first constant represents the letter a, the second is a semicolon, and the third is the character zero—which is not the same as the number zero. Do not confuse a character constant, which is a single character enclosed in single quotes, with a character string, which is any number of characters enclosed in double quotes.
1. Appendix A discusses methods for storing characters from extended character sets, through special escape sequences, universal characters, and wide characters.
The character constant '\n'—the newline character—is a valid character constant even though it seems to contradict the rule cited previously. This is because the backslash character is a special character in the C system and does not actually count as a character. In other words, the C compiler treats the character '\n' as a single character, even though it is actually formed by two characters. There are other special characters that are initiated with the backslash character. Consult Appendix A, “C Language Summary,” for a complete list.
The format characters %c can be used in a printf() call to display the value of a char variable at the terminal.
A _Bool variable is defined in the language to be large enough to store just the values 0 and 1. The precise amount of memory that is used is unspecified. _Bool variables are used in programs that need to indicate a Boolean condition. For example, a variable of this type might be used to indicate whether all data has been read from a file.
By convention, 0 is used to indicate a false value, and 1 indicates a true value. When assigning a value to a _Bool variable, a value of 0 is stored as 0 inside the variable, whereas any nonzero value is stored as 1.
To make it easier to work with _Bool variables in your program, the standard header file <stdbool.h> defines the values bool, true, and false. An example of this is shown in Program 5.10A in Chapter 5, “Making Decisions.”
In Program 3.1, the basic C data types are used.
Program 3.1 Using the Basic Data Types
Program 3.1 Output
integerVar = 100
floatingVar = 331.790009
doubleVar = 8.440000e+11
doubleVar = 8.44e+11
charVar = W
boolVar = 0;
The first statement of Program 3.1 declares the variable integerVar to be an integer variable and also assigns to it an initial value of 100, as if the following two statements had been used instead:
int integerVar;
integerVar = 100;
In the second line of the program’s output, notice that the value of 331.79, which is assigned to floatingVar, is actually displayed as 331.790009. In fact, the actual value displayed is dependent on the particular computer system you are using. The reason for this inaccuracy is the particular way in which numbers are internally represented inside the computer. You have probably come across the same type of inaccuracy when dealing with numbers on your pocket calculator. If you divide 1 by 3 on your calculator, you get the result .33333333, with perhaps some additional 3s tacked on at the end. The string of 3s is the calculator’s approximation to one third. Theoretically, there should be an infinite number of 3s. But the calculator can hold only so many digits, thus the inherent inaccuracy of the machine. The same type of inaccuracy applies here: Certain floating-point values cannot be exactly represented inside the computer’s memory.
When displaying the values of float or double variables, you have the choice of three different formats. The %f characters are used to display values in a standard manner. Unless told otherwise, printf() always displays a float or double value to six decimal places rounded. You see later in this chapter how to select the number of decimal places that are displayed.
The %e characters are used to display the value of a float or double variable in scientific notation. Once again, six decimal places are automatically displayed by the system.
With the %g characters, printf() chooses between %f and %e and also automatically removes from the display any trailing zeroes. If no digits follow the decimal point, it doesn’t display that either.
In the next-to-last printf() statement, the %c characters are used to display the single character 'W' that you assigned to charVar when the variable was declared. Remember that whereas a character string (such as the first argument to printf()) is enclosed within a pair of double quotes, a character constant must always be enclosed within a pair of single quotes.
The last printf() shows that a _Bool variable can have its value displayed using the integer format characters %i.
If the specifier long is placed directly before the int declaration, the declared integer variable is of extended range on some computer systems. An example of a long int declaration might be
long int factorial;
This declares the variable factorial to be a long integer variable. As with floats and doubles, the particular accuracy of a long variable depends on your particular computer system. On many systems, an int and a long int have the same range and either can be used to store integer values up to 32-bits wide (231 − 1, or 2,147,483,647).
A constant value of type long int is formed by optionally appending the letter L (upper- or lowercase) onto the end of an integer constant. No spaces are permitted between the number and the L. So, the declaration
long int numberOfPoints = 131071100L;
declares the variable numberOfPoints to be of type long int with an initial value of 131,071,100.
To display the value of a long int using printf(), the letter l is used as a modifier before the integer format characters i, o, and x. This means that the format characters %li can be used to display the value of a long int in decimal format, the characters %lo can display the value in octal format, and the characters %lx can display the value in hexadecimal format.
There is also a long long integer data type, so
long long int maxAllowedStorage;
declares the indicated variable to be of the specified extended accuracy, which is guaranteed to be at least 64 bits wide. Instead of a single letter l, two ls are used in the printf string to display long long integers, as in "%lli".
The long specifier is also allowed in front of a double declaration, as follows:
long double US_deficit_2004;
A long double constant is written as a floating constant with the letter l or L immediately following, such as
1.234e+7L
To display a long double, the L modifier is used. So, %Lf displays a long double value in floating-point notation, %Le displays the same value in scientific notation, and %Lg tells printf() to choose between %Lf and %Le.
The specifier short, when placed in front of the int declaration, tells the C compiler that the particular variable being declared is used to store fairly small integer values. The motivation for using short variables is primarily one of conserving memory space, which can be an issue in situations in which the program needs a lot of memory and the amount of available memory is limited.
On some machines, a short int takes up half the amount of storage as a regular int variable does. In any case, you are guaranteed that the amount of space allocated for a short int will not be less than 16 bits.
There is no way to explicitly write a constant of type short int in C. To display a short int variable, place the letter h in front of any of the normal integer conversion characters: %hi, %ho, or %hx. Alternatively, you can also use any of the integer conversion characters to display short ints, due to the way they can be converted into integers when they are passed as arguments to the printf() routine.
The final specifier that can be placed in front of an int variable is used when an integer variable will be used to store only positive numbers. The declaration
unsigned int counter;
declares to the compiler that the variable counter is used to contain only positive values. By restricting the use of an integer variable to the exclusive storage of positive integers, the accuracy of the integer variable is extended.
An unsigned int constant is formed by placing the letter u (or U) after the constant, as follows:
0x00ffU
You can combine the letters u (or U) and l (or L) when writing an integer constant, so
20000UL
tells the compiler to treat the constant 20000 as an unsigned long.
An integer constant that’s not followed by any of the letters u, U, l, or L and that is too large to fit into a normal-sized int is treated as an unsigned int by the compiler. If it’s too small to fit into an unsigned int, the compiler treats it as a long int. If it still can’t fit inside a long int, the compiler makes it an unsigned long int. If it doesn’t fit there, the compiler treats it as a long long int if it fits, and as an unsigned long long int otherwise.
When declaring variables to be of type long long int, long int, short int, or unsigned int, you can omit the keyword int. Therefore, the unsigned variable counter could have been equivalently declared as follows:
unsigned counter;
You can also declare char variables to be unsigned.
The signed qualifier can be used to explicitly tell the compiler that a particular variable is a signed quantity. Its use is primarily in front of the char declaration, and further discussion is deferred until Chapter 13, “More on Data Types.”
Don’t worry if the discussions of these specifiers seem a bit esoteric to you at this point. In later sections of this book, many of these different types are illustrated with actual program examples. Chapter 13 goes into more detail about data types and conversions.
Table 3.1 summarizes the basic data types and qualifiers.
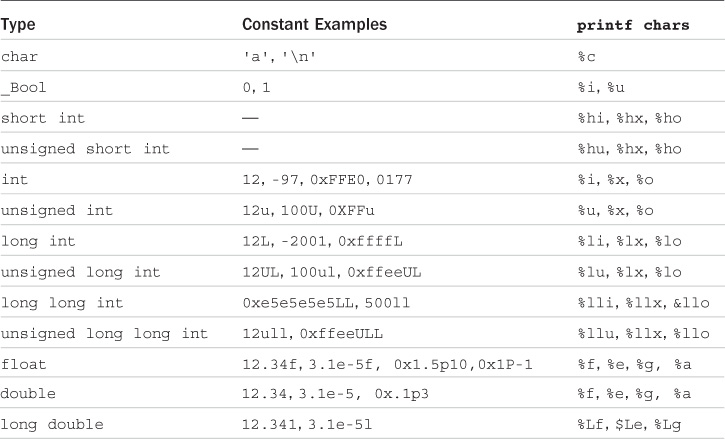
Table 3.1 Basic Data Types
Early computer programmers had the onerous task of having to write their programs in the binary language of the machine they were programming. This meant that computer instructions had to be hand-coded into binary numbers by the programmer before they could be entered into the machine. Furthermore, the programmer had to explicitly assign and reference any storage locations inside the computer’s memory by a specific number or memory address.
Today’s programming languages allow you to concentrate more on solving the particular problem at hand than worrying about specific machine codes or memory locations. They enable you to assign symbolic names, known as variable names, for storing program computations and results. A variable name can be chosen by you in a meaningful way to reflect the type of value that is to be stored in that variable.
In Chapter 2, “Compiling and Running Your First Program,” you used several variables to store integer values. For example, you used the variable sum in Program 2.4 to store the result of the addition of the two integers 50 and 25.
The C language allows data types other than just integers to be stored in variables as well, provided the proper declaration for the variable is made before it is used in the program. Variables can be used to store floating-point numbers, characters, and even pointers to locations inside the computer’s memory.
The rules for forming variable names are quite simple: They must begin with a letter or underscore ( _ ) and can be followed by any combination of letters (upper- or lowercase), underscores, or the digits 0–9. The following is a list of valid variable names.
sum
pieceFlag
i
J5x7
Number_of_moves
_sysflag
On the other hand, the following variable names are not valid for the stated reasons:

int cannot be used as a variable name because its use has a special meaning to the C compiler. This use is known as a reserved name or reserved word. In general, any name that has special significance to the C compiler cannot be used as a variable name. Appendix A provides a complete list of such reserved names.
You should always remember that upper- and lowercase letters are distinct in C. Therefore, the variable names sum, Sum, and SUM each refer to a different variable.
Your variable names can be as long as you want, although only the first 63 characters might be significant, and in some special cases (as described in Appendix A), only the first 31 characters might be significant. It’s typically not practical to use variable names that are too long—just because of all the extra typing you have to do. For example, although the following line is valid
theAmountOfMoneyWeMadeThisYear = theAmountOfMoneyLeftAttheEndOfTheYear –
theAmountOfMoneyAtTheStartOfTheYear;
this line
moneyMadeThisYear = moneyAtEnd – moneyAtStart;
conveys almost as much information in much less space.
When deciding on the choice of a variable name, keep one recommendation in mind—don’t be lazy. Pick names that reflect the intended use of the variable. The reasons are obvious. Just as with comments, meaningful variable names can dramatically increase the readability of a program and pay off in the debug and documentation phases. In fact, the documentation task is probably greatly reduced because the program is more self-explanatory.
In C, just as in virtually all programming languages, the plus sign (+) is used to add two values, the minus sign (−) is used to subtract two values, the asterisk (*) is used to multiply two values, and the slash (/) is used to divide two values. These operators are known as binary arithmetic operators because they operate on two values or terms.
You have seen how a simple operation such as addition can be performed in C. Program 3.2 further illustrates the operations of subtraction, multiplication, and division. The last two operations performed in the program introduce the notion that one operator can have a higher priority, or precedence, over another operator. In fact, each operator in C has a precedence associated with it. This precedence is used to determine how an expression that has more than one operator is evaluated: The operator with the higher precedence is evaluated first. Expressions containing operators of the same precedence are evaluated either from left to right or from right to left, depending on the operator. This is known as the associative property of an operator. Appendix A provides a complete list of operator precedences and their rules of association.
Program 3.2 Using the Arithmetic Operators
Program 3.2 Output
a - b = 98
b * c = 50
a / c = 4
a + b * c = 150
a * b + c * d = 300
After declaring the integer variables a, b, c, d, and result, the program assigns the result of subtracting b from a to result and then displays its value with an appropriate printf() call.
The next statement
result = b * c;
has the effect of multiplying the value of b by the value of c and storing the product in result. The result of the multiplication is then displayed using a printf() call that should be familiar to you by now.
The next program statement introduces the division operator—the slash. The result of 4, as obtained by dividing 100 by 25, is displayed by the printf() statement immediately following the division of a by c.
On some computer systems, attempting to divide a number by zero results in abnormal termination of the program.2 Even if the program does not terminate abnormally, the results obtained by such a division will be meaningless.
2. This happens using the gcc compiler under Windows. On Unix systems, the program might not terminate abnormally, and might give 0 as the result of an integer division by zero and “Infinity” as the result of a float division by zero.
In Chapter 5, you see how you can check for division by zero before the division operation is performed. If it is determined that the divisor is zero, an appropriate action can be taken and the division operation can be averted.
The expression
a + b * c
does not produce the result of 2550 (102 × 25); rather, the result as displayed by the corresponding printf() statement is shown as 150. This is because C, like most other programming languages, has rules for the order of evaluating multiple operations or terms in an expression. Evaluation of an expression generally proceeds from left to right. However, the operations of multiplication and division are given precedence over the operations of addition and subtraction. Therefore, the expression
a + b * c
is evaluated as
a + (b * c)
by the C programming language. (This is the same way this expression would be evaluated if you were to apply the basic rules of algebra.)
If you want to alter the order of evaluation of terms inside an expression, you can use parentheses. In fact, the expression listed previously is a perfectly valid C expression. Thus, the statement
result = a + (b * c);
could have been substituted in Program 3.2 to achieve identical results. However, if the expression
result = (a + b) * c;
were used instead, the value assigned to result would be 2550 because the value of a (100) would be added to the value of b (2) before multiplication by the value of c (25) would take place. Parentheses can also be nested, in which case evaluation of the expression proceeds outward from the innermost set of parentheses. Just be certain you have as many closed parentheses as you have open ones.
You will notice from the last statement in Program 3.2 that it is perfectly valid to give an expression as an argument to printf() without having to first assign the result of the expression evaluation to a variable. The expression
a * b + c * d
is evaluated according to the rules stated previously as
(a * b) + (c * d)
or
(100 * 2) + (25 * 4)
The result of 300 is handed to the printf() routine.
Program 3.3 reinforces what you just learned and introduces the concept of integer arithmetic.
Program 3.3 More Examples with Arithmetic Operators
Program 3.3 Output
6 + a / 5 * b = 16
a / b * b = 24
c / d * d = 25.000000
-a = -25
Extra blank spaces are inserted between int and the declaration of a, b, c, and d in the first four statements to align the declaration of each variable. This helps make the program more readable. You also might have noticed in each program presented thus far that a blank space was placed around each operator. This, too, is not required and is done solely for aesthetic reasons. In general, you can add extra blank spaces just about anywhere that a single blank space is allowed. A few extra presses of the spacebar prove worthwhile if the resulting program is easier to read.
The expression in the first printf() call of Program 3.3 reinforces the notion of operator precedence. Evaluation of this expression proceeds as follows:
1. Because division has higher precedence than addition, the value of a (25) is divided by 5 first. This gives the intermediate result of 5.
2. Because multiplication also has higher precedence than addition, the intermediate result of 5 is next multiplied by 2, the value of b, giving a new intermediate result of 10.
3. Finally, the addition of 6 and 10 is performed, giving a final result of 16.
The second printf() statement introduces a new twist. You would expect that dividing a by b and then multiplying by b would return the value of a, which has been set to 25. But this does not seem to be the case, as shown by the output display of 24. It might seem like the computer lost a bit somewhere along the way. The fact of the matter is that this expression was evaluated using integer arithmetic.
If you glance back at the declarations for the variables a and b, you will recall that they were both declared to be of type int. Whenever a term to be evaluated in an expression consists of two integers, the C system performs the operation using integer arithmetic. In such a case, all decimal portions of numbers are lost. Therefore, when the value of a is divided by the value of b, or 25 is divided by 2, you get an intermediate result of 12 and not 12.5 as you might expect. Multiplying this intermediate result by 2 gives the final result of 24, thus explaining the “lost” digit. Don’t forget that if you divide two integers, you always get an integer result. In addition, keep in mind that no rounding occurs, the decimal value is simply dropped, so integer division that ends up with 12.01, 12.5, or 12.99 will end up with the same value—12.
As you can see from the next-to-last printf() statement in Program 3.3, if you perform the same operation using floating-point values instead of integers, you obtain the expected result.
The decision of whether to use a float variable or an int variable should be made based on the variable’s intended use. If you don’t need any decimal places, use an integer variable. The resulting program is more efficient—that is, it executes more quickly on many computers. On the other hand, if you need the decimal place accuracy, the choice is clear. The only question you then must answer is whether to use a float, double, or long double. The answer to this question depends on the desired accuracy of the numbers you are dealing with, as well as their magnitude.
In the last printf() statement, the value of the variable a is negated by use of the unary minus operator. A unary operator is one that operates on a single value, as opposed to a binary operator, which operates on two values. The minus sign actually has a dual role: As a binary operator, it is used for subtracting two values; as a unary operator, it is used to negate a value.
The unary minus operator has higher precedence than all other arithmetic operators, except for the unary plus operator (+), which has the same precedence. So the expression
c = -a * b;
results in the multiplication of −a by b. Once again, in Appendix A you will find a table summarizing the various operators and their precedences.
A surprisingly valuable operator, one you may not have experience with, is the modulus operator, which is symbolized by the percent sign (%). Try to determine how this operator works by analyzing Program 3.4.
Program 3.4 Illustrating the Modulus Operator
Program 3.4 Output
a = 25, b = 5, c = 10, and d = 7
a % b = 0
a % c = 5
a % d = 4
a / d * d + a % d = 25
The first statement inside main() defines and initializes the variables a, b, c, and d in a single statement.
For a reminder, before a series of statements that use the modulus operator are printed, the first printf() statement prints the values of the four variables used in the program. It’s not crucial, but it’s a nice reminder to help someone follow along with your program. For the remaining printf() lines, as you know, printf() uses the character that immediately follows the percent sign to determine how to print the next argument. However, if it is another percent sign that follows, the printf() routine takes this as an indication that you really intend to display a percent sign and inserts one at the appropriate place in the program’s output.
You are correct if you concluded that the function of the modulus operator % is to give the remainder of the first value divided by the second value. In the first example, the remainder after 25 is divided by 5 and is displayed as 0. If you divide 25 by 10, you get a remainder of 5, as verified by the second line of output. Dividing 25 by 7 gives a remainder of 4, as shown in the third output line.
The last line of output in Program 3.4 requires a bit of explanation. First, you will notice that the program statement has been written on two lines. This is perfectly valid in C. In fact, a program statement can be continued to the next line at any point at which a blank space could be used. (An exception to this occurs when dealing with character strings—a topic discussed in Chapter 9, “Character Strings.”) At times, it might not only be desirable, but perhaps even necessary, to continue a program statement onto the next line. The continuation of the printf() call in Program 3.4 is indented to visually show that it is a continuation of the preceding program statement.
Turn your attention to the expression evaluated in the final statement. You will recall that any operations between two integer values in C are performed with integer arithmetic. Therefore, any remainder resulting from the division of two integer values is simply discarded. Dividing 25 by 7, as indicated by the expression a / d, gives an intermediate result of 3. Multiplying this value by the value of d, which is 7, produces the intermediate result of 21. Finally, adding the remainder of dividing a by d, as indicated by the expression a % d, leads to the final result of 25. It is no coincidence that this value is the same as the value of the variable a. In general, the expression
a / b * b + a % b
will always equal the value of a, assuming of course that a and b are both integer values. In fact, the modulus operator % is defined to work only with integer values.
As far as precedence is concerned, the modulus operator has equal precedence to the multiplication and division operators. This implies, of course, that an expression such as
table + value % TABLE_SIZE
will be evaluated as
table + (value % TABLE_SIZE)
To effectively develop C programs, you must understand the rules used for the implicit conversion of floating-point and integer values in C. Program 3.5 demonstrates some of the simple conversions between numeric data types. You should note that some compilers might give warning messages to alert you of the fact that conversions are being performed.
Program 3.5 Converting Between Integers and Floats
Program 3.5 Output
123.125000 assigned to an int produces 123
-150 assigned to a float produces -150.000000
-150 divided by 100 produces -1.000000
-150 divided by 100.0 produces -1.500000
(float) -150 divided by 100 produces -1.500000
Whenever a floating-point value is assigned to an integer variable in C, the decimal portion of the number gets truncated. So, when the value of f1 is assigned to i1 in the previous program, the number 123.125 is truncated, which means that only its integer portion, or 123, is stored in i1. The first line of the program’s output verifies that this is the case.
Assigning an integer variable to a floating variable does not cause any change in the value of the number; the value is simply converted by the system and stored in the floating variable. The second line of the program’s output verifies that the value of i2 (−150) was correctly converted and stored in the float variable f1.
The next two lines of the program’s output illustrate two points that must be remembered when forming arithmetic expressions. The first has to do with integer arithmetic, which was previously discussed in this chapter. Whenever two operands in an expression are integers (and this applies to short, unsigned, long, and long long integers as well), the operation is carried out under the rules of integer arithmetic. Therefore, any decimal portion resulting from a division operation is discarded, even if the result is assigned to a floating variable (as you did in the program). Therefore, when the integer variable i2 is divided by the integer constant 100, the system performs the division as an integer division. The result of dividing −150 by 100, which is −1, is, therefore, the value that is stored in the float variable f1.
The next division performed in the previous listing involves an integer variable and a floating-point constant. Any operation between two values in C is performed as a floating-point operation if either value is a floating-point variable or constant. Therefore, when the value of i2 is divided by 100.0, the system treats the division as a floating-point division and produces the result of −1.5, which is assigned to the float variable f1.
The last division operation from Program 3.5 that reads
f2 = (float) i2 / 100; // type cast operator
introduces the type cast operator. The type cast operator has the effect of converting the value of the variable i2 to type float for purposes of evaluation of the expression. In no way does this operator permanently affect the value of the variable i2; it is a unary operator that behaves like other unary operators. Because the expression −a has no permanent effect on the value of a, neither does the expression (float) a.
The type cast operator has a higher precedence than all the arithmetic operators except the unary minus and unary plus. Of course, if necessary, you can always use parentheses in an expression to force the terms to be evaluated in any desired order.
As another example of the use of the type cast operator, the expression
(int) 29.55 + (int) 21.99
is evaluated in C as
29 + 21
because the effect of casting a floating value to an integer is one of truncating the floating-point value. The expression
(float) 6 / (float) 4
produces a result of 1.5, as does the following expression:
(float) 6 / 4
The C language permits you to join the arithmetic operators with the assignment operator using the following general format: op=
In this format, op is any of the arithmetic operators, including +, −, ×, /, and %. In addition, op can be any of the bit operators for shifting and masking, which is discussed later.
Consider this statement:
count += 10;
The effect of the so-called “plus equals” operator += is to add the expression on the right side of the operator to the expression on the left side of the operator and to store the result back into the variable on the left-hand side of the operator. So, the previous statement is equivalent to this statement:
count = count + 10;
The expression
counter -= 5
uses the “minus equals” assignment operator to subtract 5 from the value of counter and is equivalent to this expression:
counter = counter - 5
A slightly more involved expression is
a /= b + c
which divides a by whatever appears to the right of the equal sign—or by the sum of b and c—and stores the result in a. The addition is performed first because the addition operator has higher precedence than the assignment operator. In fact, all operators but the comma operator have higher precedence than the assignment operators, which all have the same precedence.
In this case, this expression is identical to the following:
a = a / (b + c)
The motivation for using assignment operators is threefold. First, the program statement becomes easier to write because what appears on the left side of the operator does not have to be repeated on the right side. Second, the resulting expression is usually easier to read. Third, the use of these operators can result in programs that execute more quickly because the compiler can sometimes generate less code to evaluate an expression.
Before leaving this chapter it is worthy to note two other types in the language called _Complex and _Imaginary for working with complex and imaginary numbers.
Support for _Complex and _Imaginary types has been part of the ANSI C standard since C99, although C11 does make it optional. The best way to know if your compiler supports these types is to examine the summary of data types in Appendix A.
Using Variables, Data Types, and Expressions
1. Type in and run the five programs presented in this chapter. Compare the output produced by each program with the output presented after each program in the text.
2. Which of the following are invalid variable names? Why?
Int char 6_05
Calloc Xx alpha_beta_routine
floating _1312 z
ReInitialize _ A$
3. Which of the following are invalid constants? Why?
123.456 0x10.5 0X0G1
0001 0xFFFF 123L
0Xab05 0L -597.25
123.5e2 .0001 +12
98.6F 98.7U 17777s
0996 -12E-12 07777
1234uL 1.2Fe-7 15,000
1.234L 197u 100U
0XABCDEFL 0xabcu +123
4. Write a program that converts 27® from degrees Fahrenheit (F) to degrees Celsius (C) using the following formula:
C = (F - 32) / 1.8
5. What output would you expect from the following program?
#include <stdio.h>
int main (void)
{
char c, d;
c = 'd';
d = c;
printf ("d = %c\n", d);
return 0;
}
6. Write a program to evaluate the polynomial shown here:
3x3 - 5x2 + 6
for x = 2.55.
7. Write a program that evaluates the following expression and displays the results (remember to use exponential format to display the result):
(3.31 x 10-8 x 2.01 x 10-7) / (7.16 x 10-6 + 2.01 x 10-8)
8. To round off an integer i to the next largest even multiple of another integer j, the following formula can be used:
Next_multiple = i + j - i % j
For example, to round off 256 days to the next largest number of days evenly divisible by a week, values of i = 256 and j = 7 can be substituted into the preceding formula as follows:
Next_multiple = 256 + 7 - 256 % 7
= 256 + 7 - 4
= 259
9. Write a program to find the next largest even multiple for the following values of i and j:
